Muchos nos escandalizamos al ver publicadas en los medios burdas manipulaciones que hacen uso de la estadística para hacer que los datos acaben confesando cualquier cosa que interese a la línea editorial del medio. Quienes las escriben en informes, estudios o las comunican en ruedas de prensa probablemente lo hacen a sabiendas de que están manipulando la información, pero me queda la esperanza de que los periodistas que les dan difusión no son nada críticos por simple desconocimiento de que están siendo manipulados.
A pesar del título, mi intención con esta «guía» es simplemente reclamar el uso del sentido común tanto por parte del periodista que escribe en un importante medio de comunicación (es una gran responsabilidad) como por cualquiera de los que los leemos (es nuestra obligación ser críticos).
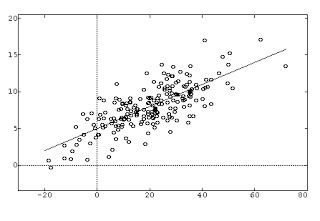 |
| Ejemplo de regresión lineal, una manera clásica de aproximar datos por una línea |
En concreto, me centraré en la parte del sentido común que se llama matemática estadística. Sí: las matemáticas no son más que cadenas de razonamientos basados en una forma de pensar «lógica» y ordenada. No hay nada raro, cualquiera puede entenderlo sin tener dos doctorados ni tres masters, en serio. Por eso he intentado evitar en toda esta guía palabrejas raras mientras ha sido posible, sustituyéndolas por ejemplos y explicaciones que espero sean asequibles a cualquiera.
Empezamos por los conceptos más simples y llegaremos a algunos un poquito más abstractos, pero no por ello menos importantes (¡todo lo contrario!).
1. Porcentajes
Es algo extremadamente básico, pero a gente que no es «de ciencias» les cuesta mucho estar seguros de interpretar o calcular bien un simple porcentaje.
Pasar de números a porcentajes:
Si tenemos un total de N elementos, y queremos calcular qué porcentaje representan K elementos, lo que se hace en realidad es una regla de tres, cogiendo la proporción que hay entre K y N, y llevándola al caso en que N es 100 (por eso se llama porcentaje, de cien). En forma de regla de tres de la que enseñan en el colegio, sería:
Que se resuelve igualando la relación (fracción) de cada lado:
que se despeja multiplicando por 100 en ambos lados. Es decir, el porcentaje se calcula dividiendo K entre N y multiplicando por 100:
Ejemplo: De un total de 140.000 votos un partido obtiene 35.000, o en porcentaje:
Pasar de porcentajes a números:
Si tenemos un porcentaje p (en tanto por ciento, %) y queremos saber cuántos elementos representan de un total de N:
Ejemplo: De un total de 47 millones de españoles, un 21,8% viven bajo el umbral de la pobreza, por lo que en número de personas:
2. Porcentajes encadenados y relativos
Porcentajes encadenados:
A veces se hace referencia a un porcentaje dentro de otro porcentaje, como en: «un 20% de la población está en paro, y de esos, un 40% tienen hijos a su cargo» (¡datos inventados!). Si queremos saber a cuántas personas se refiere ese 40%, con respecto al total de la población, tenemos que multiplicar porcentajes, aunque eso sí, pasándolos antes a tantos por uno, para finalmente convertirlos de nuevo a tantos por cien.
Un ejemplo: Para el caso de antes, tenemos que pasar ambos porcentajes a tantos por uno:
Ahora los multiplicamos:
Y lo pasamos a tanto por cien:
Es decir, que el 40% del 20% es un 8% del total. La misma idea se puede repetir para más de dos porcentajes encadenados hasta el número de encadenamientos que se quiera.
Porcentajes relativos:
Con «relativos» me refiero a esas veces en que queremos decir cuánto ha aumentado o disminuido una cantidad. Por ejemplo, «la empresa X ha ganado este año un 10% más que el año anterior», o «el número de accidentes se ha reducido en un 20%».
Si tenemos los datos en bruto del antes y después, el porcentaje se calcula pasando a porcentaje la diferencia entre ambos datos, relativos al valor inicial, ¡ojo!.
Ejemplo 1: De ganar 2000€ ha pasado a ganar 2300€, con lo que:
Ejemplo 2: De ganar 2300€ ha pasado a ganar 2000€, con lo que:
3. ¡Es exponencial, maldita sea!
Continuando con el tema anterior, hay un fallo tremendamente común, relacionado con series de incrementos en porcentajes. Imagina que el PIB de un país, o las ganancias de una empresa, siguen esta secuencia:
2005: +4%
2006: +5%
2007: +6%
2008: +5%
Lo más normal es encontrarse titulares como:
En 2008 se creció menos que en 2007
Pues hay que tener muy claro que porque 5% sea menos de 6% ¡¡eso no tiene por qué decir que se haya crecido menos!!
La cuestión es que el 6% de 2007 se calculó como el crecimiento sobre el total de 2006, pero el crecimiento de 2008 se calculó sobre el total de 2007… ¡que era mayor que el de 2006!
En cada caso habría que echar números y ver cuánto se creció cada año en valor absoluto (no en porcentaje) usando las fórmulas del punto 1, y esas cantidades son las que habría que comparar.
Otro concepto que es común no entender es el de «crecimiento constante«, que comúnmente (y erróneamente) se asocia a un crecimiento en porcentaje constante a lo largo de los años. Es decir, un «crecimiento constante» del PIB de un país NO consiste en crecer todos los años un 2%, ni un 1% ni ningún otro porcentaje… Si se piensa, se verá claro que en realidad crecer un X% todos los años cada vez cuesta más, porque se aplica al valor total del año anterior, que cada vez es más grande. En realidad, un «crecimiento constante en porcentaje» implica un crecimiento en valor absoluto exponencial, que no es una evolución en línea recta ni mucho menos:
 |
| Ejemplo de función exponencial (fuente) |
Como dato para reflexionar: ningún proceso en la Naturaleza es capaz de aguantar creciendo exponencialmente de manera indefinida.
Si tenemos un gran número de datos, miles o millones de ellos, necesitamos resumirlos de alguna forma porque sino nunca podríamos analizarlos ni entender cómo van cambiando en el tiempo.
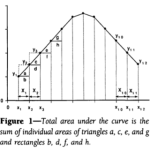
Un primer paso es ver de qué manera se distribuyen los números, en lo que se llama distribución de probabilidad. Para entender qué significa esto, imagina una gráfica, en el que el eje horizontal representa los valores de los datos (p.ej. la edad de una población, la nota de los alumnos, etc.). Si ahora dividimos ese eje en trocitos o segmentos y vamos contando cuántos datos caen en cada uno de esos trocitos, acabamos teniendo un número en cada segmento, que podemos dibujar como una altura vertical. Esto se llama histograma:
 |
| Distribución Gausiana (fuente) |
Esa forma gráfica nos da una enorme cantidad de información. Si aparece un único pico, como en el dibujo de arriba, significa que existe un valor «normal» alrededor del cuál están el resto, y que existe solamente una minoría lejos de ese valor.
No siempre tiene que ser así, ya que por ejemplo pueden existir dos picos, que significaría que los datos se pueden agrupar en torno a dos o más «modos». En este ejemplo se ven dos modos (distribución bimodal):
 |
| Distribución bimodal (fuente) |
Pues bien, los histogramas, cuando el tamaño de los segmentos se va reduciendo hasta llegar a ser minúsculos, es lo que se llama función de densidad de probabilidad (fdp). Por ese nombre quizás no os suene, pero la más conocida seguro que te resulta familiar: distribución Gausiana o normal.
Conocer el histograma o fdp es conocer perfectamente los datos. Pero lamentablemente, nunca se publican. Es mucho más rápido dar una serie de números que resumen la información de los histogramas (los «momentos«). El más usado de todos es el valor medio. Es un concepto muy útil pero puede ser tremendamente engañoso.
La media de una serie de datos es simplemente la suma de todos ellos, dividido por el número de datos. Si los datos realmente sólo tienen un pico (primera figura de arriba), la media estará muy cerca de ese pico. Pero si en cambio tiene varios picos (segunda figura) la media nos saldrá en mitad de los picos, en un valor que quizás no es nada común.
Esto es por ejemplo lo que ocurre con los salarios medios, donde, cada vez más, existen dos picos (los sueldos extraordinariamente altos, y los modestos de las clases populares) por lo que ese salario medio realmente es cada vez menos significativos.
Por favor, periodistas: siempre, siempre, siempre, pedid, exigid los histogramas completos de los datos, ya que es la información más verídica. Si eso no es posible, al menos pedid la desviación estándar de los datos. Una media y una desviación estándar da una idea mucho más precisa de los datos que únicamente la media.
5. Dar datos significativos en comparaciones
Este punto es más de sentido común que de conceptos matemáticos propiamente dichos.
Manipulación/error de tipo 1: No dar toda la información. Como ejemplo, este titular:
Las comunidades autónomas gobernadas por el partido de Rajoy gastaron en el primer trimestre un 10,1% más, casi el cuádruple que el resto (2,6%)
Obviamente se trata de un intento de manipulación (espero que nadie se ofenda por elegir ese periódico en particular, existen errores en todos ellos). El hecho numérico está ahí y nadie lo puede negar, pero habría que analizar:
- ¿De qué depende el gasto? Tamaño de población, gasto en infraestructuras, etc.
- ¿De qué presupuestos partían el año anterior? Si el resto ha aumentado un 2,6%, quizás aún así sigan estando muy por encima del valor absoluto (o incluso en gasto medio por habitante) de las comunidades a las que se pretende criticar.
Explicado sin términos matemáticos, en lenguaje llano: si tenemos un dato cuya componente aleatoria, de azar, es más grande que la diferencia entre meses o entre años, sencillamente no podemos decir si sube o baja, al menos no con rotundidad. Hay que ser prudente al realizar afirmaciones sobre datos muy variables.
Ejemplo: Decir a media mañana que las acciones de la compañía X han subido o bajado un 0.5% con respecto al día anterior, pues como que no tiene mucho sentido si se está viendo que antes ha oscilado entre un -3% y un +3% en unas pocas horas.
Un ejemplo:
- «El estado de la economía es malo, hay un 20% de paro».
- «El estado de la economía es apocalíptico: hay un 20% de paro, un 15% de hogares sin ningún ingreso, los pequeños hurtos han subido un 40% y las colas en comedores sociales han aumentado un 35%».
Todos los hechos del segundo punto realmente se podrían trazar a un único origen (quizás, el problema del paro), por lo que no aportan nada nuevo: son solamente reflejos de un mismo hecho.
Resumen de la idea: Varios datos estadísticos se pueden sumar al apoyo de una tesis sólo si reflejan hechos totalmente independientes.
Ya hemos visto arriba que la media puede dar una buena idea de por dónde van los datos… sólo si existe un único «modo», es decir, todos los datos están aproximadamente centrados en torno a un valor.
A veces se utilizan los valores medios para hacer cuentas, y con eso sacar supuestos valores medios de otros conceptos. Pues bien:
Uno puede sentirse tentado de obtener los siguientes datos:
- Sm = Sueldo medio mensual en un país.
- P = Precio de los 100 litros de gasolina que se suponen el estándar de gasto mensual.
Para entender donde está el problema, empecemos por el principio. Si «S» es el sueldo de una persona en particular (no el medio de un país), entonces sí que el porcentaje de sueldo que se le va en gasolina es:
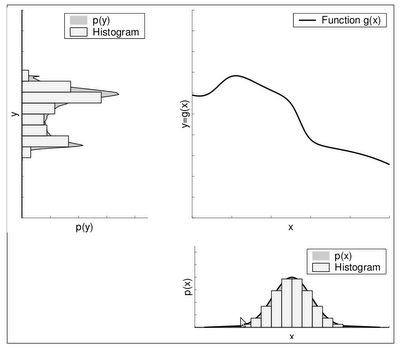 |
| (Fuente) |
En mi opinión, el ejemplo por antonomasia de este tipo de «error», casi en clave de humor, es:
El tamaño del pene está relacionado con el crecimiento del PIB: Un investigador de la Universidad de Helsinki (Finlandia) ha llegado a la conclusión en un reciente estudio que el tamaño promedio del pene en un país, tiene directa relación con el crecimiento del Producto Interno Bruto (PIB) de cada nación.
Aunque hay que reconocer que el estudio no parece achacar que el tamaño del pene sea la causa del mayor o menos PIB del país, la forma de presentarlo puede hacer creer al lector que esa es la opinión del autor. En cambio, hay muchas otras noticias en las que el error sí aparece más claro (ejemplos: ésta o ésta)
La cuestión es simple: que se presente correlación entre dos variables no implica que esa sea el origen o la causa de ningún hecho.
Existe un fundamento matemático detrás de este razonamiento, basado en una forma de teoría de probabilidades que se llama modelos gráficos, en los que cada «hecho» se representa como un nodo y las relaciones causales entre ellas se representan por arcos.
En esta teoría matemática, imaginemos que tenemos un conjunto de 3 hechos, que afectan a un cuarto hecho, y ese, a su vez, afecta a otros tres. Eso se representaría con la figura de la izquierda:
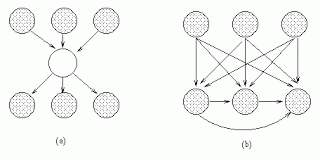 |
| Efecto de ignorar un «hecho» que vincula los tres de arriba con los tres de abajo (fuente) |
Pues bien, ojo al dato: según esta teoría de grafos, si ignoramos el hecho intermedio que aparece en blanco (lo que se llama marginalizar ese dato), e interpretamos los datos únicamente de los otros seis hechos, descubriríamos que existen correlaciones, que parecerían indicar causalidad, entre casi todos ellos. Eso se ve con las flechas de la figura de la derecha.
Moraleja de todo esto: Cuando los datos parezcan indicar causalidad entre dos hechos, nunca, repito, NUNCA, debemos descartar que realmente lo que esté ocurriendo es que hayamos olvidado tener en cuenta un hecho o factor intermedio, que realmente sea la causa última.
Con esta entrada participo en la edición 2.7 del Carnaval de Matemáticas, organizado en este blog.