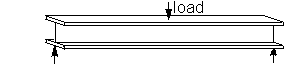Una de integrales y física: ¿Por qué los escalones metálicos tienen las formas que tienen?

El diseño científico y racional se encuentra en tantos objetos cotidianos que es fácil pasar muchos por alto. Por ejemplo, hoy vamos a ver por qué los escalones metálicos de muchas escaleras, especialmente las construidas de la forma más económica posible, ahorran material al usar esas formas típicas con ángulos en «L», «U» o «S».

Escalones metálicos, con el típico perfil en «S» (fuente)

El objetivo que se tiene en mente al diseñar un escalón metálico es, básicamente, que aguante un cierto peso sobre él sin «doblarse» (técnicamente, flectar) en exceso. El tipo de deformación, visto en perfil, es el siguiente:

Deformación del tipo «flexión» (créditos)

Saber cuánto va a flectar un elemento sólido deformable (cualquier pieza metálica es elástica y deformable) es el campo de una parte de la física llamada (¡tachán!) mecánica del sólido deformable. En la práctica, como suele pasar con todas las ciencias, las ecuaciones a las que se llega solamente tienen solución para casos idealizados («sea una vaca esférica…»), pero aún así tienen una aplicación práctica importantísima a todas las ramas de la arquitectura e ingenierías industriales, mecánica y de la construcción.

Por supuesto, el auge de los ordenadores en las últimas décadas ha permitido olvidarse de esas ecuaciones aproximadas y directamente resolver cualquier problema mediante integración numérica (dando lugar al método de los elementos finitos), pero para el tema de hoy nos basta y nos sobra con nuestras vacas esféricas.

En concreto, para ver qué le pasa a un escalón metálico, vamos a usar la (burda) aproximación de asumir que es mucho más largo que ancho, con lo que nos sirven las ecuaciones normalmente usadas para vigas en construcción.

La primera aproximación que nos permite esto es simplificar el estado de tensiones que sufre el material a lo largo de su interior, normalmente dado por un tensor de tensiones con 9 valores para cada punto del espacio,

Representación del tensor de tensiones T al cortar un sólido (fuente)

y simplificarlo, como digo, a solamente tres valores de esfuerzos (que son fuerzas, frente a las tensiones que eran fuerzas por unidad de superficie) a lo largo del eje longitudinal x:

N(x): Esfuerzo axil («paralelo al eje»)
V(x): Esfuerzo cortante («perpendicular al eje»)
M(x): Momento flector (el momento de fuerza que tiende a «doblar» el elemento)

Si estamos interesados en saber «cuánto se dobla» nuestro escalón, lo que queremos obtener es la llamada flecha (v(x)), que indica cuánto se desplaza el elemento en cada punto x con respecto a su posición inicial.

La ecuación diferencial que sigue la flecha es:

[ frac{d^2 v(x)}{dx^2} = frac{M(x)}{EI_z} ]

donde E es una constante que dice lo elástico que es el material, e (I_z) es el momento de inercia del área, al que luego volveremos porque es el quid de la cuestión.

Para determinar el valor de M(x) tenemos que saber de qué forma particular se le aplica el peso (o carga) al escalón, por lo que nos lo pondremos fácil y supondremos (otra aproximación más…) que el peso se reparte uniformente tal que q(x) nos dice cuántos kg/m aplicamos:

(Créditos)

Como se puede demostrar que la relación entre la carga q(x) y el momento es:

[frac{d^2 M(x)}{dx^2} = q(x) ]

juntamos las dos ecuaciones anteriores y llegamos a la conocida ecuación de la curva elástica:

[ frac{d^4 v(x)}{dx^4} = frac{1}{E I_z} q(x) ]

Sustituyendo ahora el valor de la carga uniforme (q(x)=q) e integrando cuatro veces, podemos sacar el valor de cuánto se desplaza el escalón en cada punto x:

[ v(x) = frac{1}{E I_z} left( frac{qx^4}{24} + frac{C_1 x^3}{6} + frac{C_2 x^2}{2} + C_3 x + C_4 right) ]

donde las (C_1, C_2, C_3, C_4 ) son constantes de integración que se sacarían a partir de las condiciones de contorno, pero no nos interesan aquí.

Por simetría, y como nos dice la intuición, el máximo desplazamiento se dará justo en el centro, y tendrá un valor (sustituyendo ya todas las constantes de integración):

[ v(frac{L}{2}) = frac{qL^4}{384 E I_z} ]

Ha costado un poco, pero ya tenemos una fórmula que nos dice exactamente de qué depende que un escalón se deforme más o menos: lo hará proporcional a la carga (¡lógico!), a la cuarta potencia con respecto a la longitud (esto se ve intuitivamente: manteniendo constante el tipo de material, cuanto más largo sea más le costará «resistir» el peso) e inversamente proporcional a las constantes E e (I_z).

La longitud del escalón L será la que haga falta cubrir, ahí no podemos hacer nada. Con respecto al módulo de elasticidad E, depende solamente del material (madera, acero,…).

Es decir, una vez decidido que por estética, conveniencia o precio se va a hacer un escalón de metal (típicamente acero), solamente podemos jugar con la constante del momento de inercia (I_z) en el diseño.

Como queremos minimizar la flexión, vemos que debemos maximizar el valor (I_z). Pero ¿qué mide este número exactamente? Matemáticamente, se define como la integral, a lo largo del área de la sección perpendicular al eje longitudinal, de la distancia al cuadrado desde el eje del sólido que se estudia:

[ I_{eje} = iint_{Sigma} r^2 dA ]

Intuitivamente, si pensamos en nuestro escalón, imaginad que le damos un «corte» con un cuchillo. Pues bien, la parte que toca el cuchillo sería la sección transversal del escalón, y (I_z) mide la propiedad geométrica de «cómo de lejos está la masa del eje».

Es decir: cuantas más partes de la sección estén lejos del centro , mayor será el momento de inercia y más resistirá a la flexión.

Exactamente esta misma razón es por lo que las vigas en construcción tienen esos perfiles donde se coloca todo el material posible lejos de su eje central:

Perfiles normalizados tipo IPE como los usados en construcción (fuente)

Obviamente, una manera equivalente de aumentar el valor de (I_z) sería lo que se le habría ocurrido a cualquiera hasta hace dos siglos: ¡hacer el escalón más gordo!

Intuitivamente, sabemos que meter más material hace cualquier pieza más rígida, pero la maravilla de la física y las matemáticas es que nos permiten apuntar con el dedo a exactamente dónde tiene que estar el material para maximizar el efecto deseado y minimizar el coste en material, no usando más del necesario.