Los ordenadores y videoconsolas, basadas en procesadores con un comportamiento 100% matemático y preciso, necesitan a veces generar aleatoriedad. Hoy traigo la historia de una de las mayores pifias que una empresa informática (IBM) haya cometido jamás relacionada con, precisamente, la falta de aleatoriedad.
Los microprocesadores no son más que circuitos electrónicos, extremadamente complejos, cuyo objetivo es simplemente mover numeritos de un lado a otro y realizar operaciones matemáticas simples con ellos. Y siempre, siguiendo algún programa preestablecido más o menos complejo y de manera incansable.
Si a un programa de ordenador se le pide que repita 100 veces un cálculo, por complejo que sea, siempre dará lugar al mismo resultado.
 |
| El problema de los números aleatorios… ¿cómo saber si realmente lo son? (Dilbert) |
Por ello, quizás pueda parecer chocante hablar de «aleatoriedad» o de programas estocásticos en un ordenador. Pero existen para cubrir unas necesidades importantes. En el cálculo científico, por citar sólo una utilidad, existen técnicas de simulación llamadas de Monte Carlo, usadas por ejemplo para que un robot móvil sepa por dónde anda y por la NASA para tener en cuenta todas las posibilidades al calcular un aterrizaje de una nave en la Luna. Los métodos Monte Carlo tienen mil y una aplicaciones más así que mejor ni empiezo a enumerarlas.
También en videojuegos generar números aleatorios es algo esencial: ¿qué pensarías de jugar al Tetris si siempre se repitiese la misma secuencia de piezas? ¿O si los enemigos de un FPS siempre se portasen exactamente igual? Perderían bastante la gracia, ¿verdad?
Existen varias maneras de emular ciertas dosis de aleatoriedad con la capacidad de cálculo puramente mecánica, repetitiva y predecible de una máquina. El objetivo es generar números que sean todo lo aleatorios que sea posible, es decir: que la probabilidad de generar cada número sea la misma para todos. Además lo suyo es que las secuencias no sean fácilmente predecibles, etc.
El método más extendido para conseguir esto se llama generador de congruencia lineal, y a pesar del nombre es más simple que el mecanismo de un botijo:
- Empezamos con un número cualquiera ( x_0 ) , que se llamará «semilla» (o seed).
- Para cada número pseudoaleatorio que se quiera generar, usar esta fórmula recursiva:
- M=231 para evitar calcular el resto: dividir por potencias de dos en informática se convierte en encender o apagar determinados «ceros y unos» en una ristra de ceros y unos en el que se puede representar cualquier número.
- A=0 para ahorrar una suma.
- B=65539 porque 65539 = 216 + 3, de nuevo simplifica las operaciones en binario.
Al algoritmo así creado se le dió el infame nombre de RANDU y ha pasado a la historia por ser el paradigma de todos los males que pueden afectar a un mal diseñado generador aleatorio. En su descargo, habría que alegar que los ordenadores de la época intentaban minimizar todos los cálculos costosos innecesarios. Pero en este caso se pasaron al buscar simplicidad sin pensar en las consecuencias. Los fallos de su algoritmo fueron:
- Sólo se puede inicializar con semillas que sean números impares.
- Las probabilidades de aparición de cualquier número par son nulas: ¡sólo genera números impares!
- Todos los generadores, al final, acaban repitiendo la secuencia (lo que se llama período del generador). Aunque podría tener un período de hasta 231, realmente empieza a repetirse bastante antes.
- Lo peor de todo: los números generados ¡tienen una fuerte correlación entre sí!
Para ilustrar este último punto quiero mostrar algunas gráficas y un vídeo. Para hacerlos, he tenido que crear una pequeña clase en C++ que implementa RANDU, así que lo dejo aquí por si a alguien le viene bien:
class RANDU
{
uint32_t seed;
public:
RANDU() : seed(1) { }
uint32_t draw()
{
return seed = (65539*seed) & 0x7FFFFFFF;
}
};
He generado 10,000 números de la secuencia que empieza con la semilla 1:
1, 65539, 393225, 1769499, 7077969, 26542323, 95552217, 334432395, 1146624417, 1722371299, 14608041, 1766175739, 1875647473, 1800754131, …
Si ahora normalizamos los números (para que estén entre 0 y 1) y los dibujamos en una gráfica unidimensional, cada uno a la derecha del otro, tenemos una imagen que aparentemente muestra números decentemente aleatorios.
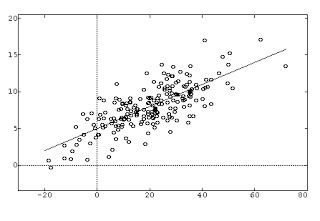
¿Y si los dibujamos de dos en dos? Podemos ir cogiendo pares de números, y cada uno será la coordenada X e Y de un punto en el plano 2D. También obtenemos algo con pinta decente de aleatorio:
¿Y de tres en tres? Ahora cada trío de números serán las coordenadas X, Y y Z de un punto. Esto obtenemos:
Tiene buena pinta… ¡hasta que lo giramos en 3D! He grabado un vídeo para ilustrar lo que ocurre:
Efectivamente: ¡todos los puntos caen en planos! Concretamente, 15 planos.
Como demuestran en la Wikipedia, se puede ver fácilmente que los parámetros usados en RANDU, operando acaban dando la siguiente fórmula recursiva:
[ x_{k+2}=6x_{k+1}-9x_{k} ]
Que es… la ecuación de un plano. Y al estar trabajando con aritmética modular ese único plano se parte en varios, que es lo que vemos en la figura.
Pero, ¿es esto tan terrible? Sí, es gravísimo: cualquier experimento científico (p.ej. Monte Carlo) que analice datos usando como fuente RANDU, acabará concluyendo que existe correlación entre las variables del estudio, no porque realmente exista, sino por culpa de los números falsamente aleatorios de entrada.
Como escribirían en el mítico Numerical Recipes veinte años después:
«si tuviéramos que eliminar todos los artículos científicos cuyas conclusiones han quedado invalidadas por culpa de usar RANDU, quedaría en cada estantería un hueco del tamaño de un puño».
Así que ya sabéis: ¡no es aleatorio todo lo que lo parece! 😉
Para acabar, mi recomendación si necesitáis un generador pseudo-aleatorio de calidad: Mersenne twister.