Una de integrales, tuberías, grietas y hielo

Hoy veremos no sólo porqué las tuberías pueden reventar a causa del hielo, lo que es muy fácil de entender, sino la sutil causa de que las grietas aparezcan siempre en una dirección concreta. La demostración matemática es asombrosamente sencilla.

¿Por qué revienta una tubería de agua si se congela?

Ésta es la parte fácil. Prácticamente todas las sustancias se dilatan al aumentar su temperatura, o lo que es lo mismo, disminuyen su volumen con el frío. Pero hay algunas excepciones, de las cuales la más trascendente sin duda es el comportamiento anómalo del agua: el hielo se dilata con respecto a su volumen equivalente en fase líquida. Por eso los cubitos de hielo flotan.

Si una tubería repleta de agua se enfría tanto como para que el agua se congele su volumen aumentará, lo que causará una presión en la cara interna de los tubos de metal que si es suficiente acabará por romper la tubería.

Tubería helada (fuente)

Y, ¿por qué revienta «a lo largo» de la tubería?

En la foto anterior se aprecia muy claramente que la grieta aparece como cortada con un cuchillo a lo largo de la tubería, en su dirección longitudinal. A priori, nada obliga a que sea así: bien podría reventar «a lo ancho» o siguiendo una trayectoria zigzageante.

La razón de la forma de estas grietas no tiene nada que ver con que el metal de la tubería sea más débil en esa dirección (si está bien fabricada no tiene porqué serlo en ninguna dirección particular), sino directamente con un principio físico muy sencillo de entender: la distribución desigual de las tensiones en el metal.

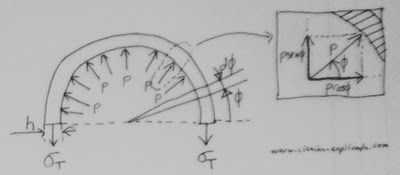
Consideremos un fragmento de una tubería sometida a presión interna, como el de la figura:

Asumiendo simetría radial en la presión que el contenido de la tubería (gas, líquido, hielo, da igual) ejerce hacia el exterior, los esfuerzos a los que estará sometida la pared de la tubería tendrán las dos componentes principales que se ven en la derecha: una tensión transversal (\(\sigma_T\)) y una longitudinal (\(\sigma_L\)). Una tensión es una magnitud física que tiene unidades de presión, p.ej. Pascales, pero no representa la acción sobre una superficie, sino la tensión interna de un material.

Llamando p a la presión ejercida por el contenido de la tubería, estudiamos primero el valor de la tensión longitudinal. Para ello, imaginemos un segmento de la tubería cerrado en sus dos extremos (¡ya que de no estar cerrados el contenido saldría y no aumentaría su presión!) como el de la izquierda:

Si pegamos un corte perpendicular al eje en cualquier punto y nos quedamos con uno de ellos (p.ej. el izquierdo), podemos deducir el valor de la tensión longitudinal a partir del principio de equilibrio de fuerzas: ya que la tubería no se mueve, todas las fuerzas horizontales en una dirección deben equilibrarse con las horizontales en dirección contraria.

En este caso tenemos la presión del contenido ejerciendo en el extremo izquierdo sobre el área circular de la «tapa» de la tubería, y por el otro, las tensiones longitudinales de la sección de la tubería (ver derecha de la figura anterior). Esta tensión existe debido al alargamiento horizontal al que es sometida la tubería por la dilatación del contenido.

La ecuación de equilibrio debe por tanto integrar las dos fuerzas repartidas, una sobre el área circular izquierda de radio R y la otra sobre la sección circular de radio interno R y grosor h. Integrando, o usando directamente las fórmulas de esas áreas (aproximando para h<<R):

\( \begin{array}{l} \sum F_{horizontales} = -p \pi R^2 + 2 \pi Rh \sigma_L = 0 \\ \rightarrow \sigma_L = \frac{p R}{2h} \end{array} \)

Ya tenemos la tensión longitudinal, vamos a por la tangencial. Para ello, pegamos ahora un corte al tubo a lo largo de un plano que pase por su eje, quedándonos con sólo media tubería. Si miramos de frente una sección de este corte tenemos la presión del contenido empujando la pared de la mitad superior y las tensiones de los dos trozos de pared que hemos cortado, tal que así:

Las fuerzas horizontales están todas en equilibrio, lo que se deduce por simetría (el lector puede hacer la integral correspondiente como ejercicio y verificar que sale cero).

Respecto a las verticales, tenemos la parte de las tensiones del tubo hacia abajo, cuyo valor sale de multiplicar la tensión (desconocida) (\(\sigma_T\)) por los dos rectángulos de extensión h (grosor) por L, siendo L una longitud de tubo (arbitraria). Es decir: (\(2 \sigma_T h L\)).

Las componentes verticales de la presión interna se puede ver en el dibujo que se corresponden con la integral, para todos los ángulos (phi) desde 0 hasta 180º ((pi ) radianes), de una presión (p sinphi ) aplicada sobre un arco de longitud (Rdphi) y longitud L (arbitraria, pero la misma que antes) .

Por equilibrio de fuerzas sabemos que ambas partes sumadas deben dar cero, así que:

\( \begin{array}{l} \sum F_{verticales} = -2 \sigma_T h L + \int_{0}^{pi}p L \sin \phi R d \phi = 0 \\ -2 \sigma_T h + p R \int_{0}^{pi} \sin \phi d \phi = 0 \\ -2 \sigma_T h + p R \left[ -\cos \phi \right]_{0}^{\pi} = 0 \\ -2 \sigma_T h + p R \left[ 1+1 \right] = 0 \\ -2 \sigma_T h + 2 p R = 0 \\ \rightarrow \sigma_T = \frac{pR}{h} \end{array} \)

En resumen,

\( \begin{array}{l} \sigma_T = \frac{pR}{h} \\ \sigma_L = \frac{p R}{2h} \end{array} \)

En palabras: la tensión tangencial es el doble de la longitudinal, lo que claramente explica que esa sea la dirección en la que primero falla el metal de una tubería congelada: «rasgándose» a lo largo de una línea longitudinal en el que la tensión tangencial empuja para abrir el metal.