Segunda parte de la serie: ¡estadística para periodistas!
Los números resultantes de hacer una medición no significan nada, a menos que conozcamos sus márgenes de error e incluso cómo se correlan entre ellas. Por obvio que parezca, es algo que se olvida a menudo.
Cuando se habla de cómo varía la intención de voto según encuestas, encontramos el término «estadísticamente significativo» en casi todos los medios internacionales (e.g. ABCNews, Washington Times, New York Times, CBS News,…).
Por el contrario, no recuerdo haber leído nunca nada parecido en un periódico español. Como ejemplo para la entrada de hoy, voy a basarme en el último artículo de El País (14/04/2012) sobre el tema (no es por nada en particular: todos los diarios parecen ignorar por igual la estadística). Veremos qué afirmaciones de las que se hacen tienen sentido y cuáles tienen el mismo valor que decir que no hay calentamiento global porque hoy hace más frío que ayer.
Las mismas ideas se podrán aplicar también a comparaciones del número de accidentes de tráfico, del valor de las acciones de un día para otro, el número de días que no ha llovido en cada año, la opinión de los españoles sobre cuáles son los principales problemas del país, etc.
1. Objetivos de esta entrada
Al terminar de leer esta entrada, sabrás:
- Qué significa, intuitiva y visualmente, la «incertidumbre» en una cifra.
- ¿A qué se refieren cuando dicen que un «margen de error» es «del 95,5%«? ¿Qué es eso de «p=q=50»? ¿Me afecta en algo? ¿Qué tiene que ver Yao Ming en todo esto? 😉
- Cómo calcular el margen de error de una encuesta, más exactamente incluso que las cifras que se suelen dar en las fichas técnicas ya que esas son para el peor caso posible.
- A interpretar si un margen de diferencia entre dos partidos o entre el mismo partido en dos momentos distintos es estadísticamente significativo.
Espero llegar al máximo número de periodistas posibles. No sé si ningún medio habla con propiedad estadística a posta (¡espero que no!) o por simple desconocimiento.
Si es lo segundo, y aparte de la reflexión de cómo es posible que no se enseñen estas cosas en las facultades de Periodismo, espero que con un mínimo, muy mínimo de esfuerzo sea posible entender lo que voy a explicar. Creo que es posible, y muy fácil, mejorar la calidad técnica de nuestras publicaciones nacionales. Al lío…
2. ¿Qué es la «incertidumbre»?
Para entender qué es un «margen de error» en una medida, también llamado «intervalo de confianza«, hay que interiorizar primero qué es la incertidumbre.
Muchas veces manejamos «valores»… de los que realmente no conocemos su valor, por mucho que sepamos por ejemplo su valor medio (p.ej. el salario medio) o una estimación (p.ej. las estimaciones de voto a partir de encuestas).
Veamos un ejemplo: si cogemos a un hombre al azar, ¿cuál sería su altura?
Según estadísticas, en EEUU la altura media está en 1 metro y 78 cm. Pero esto no responde a la pregunta, porque si empezamos a medir a gente al azar: ¿veríamos muchas alturas cerca de 1,78m? ¿habrá mucha gente que mida menos de 1,60m? Y, ¿cómo de raro es encontrar a personas de 2,29m como Yao Ming?
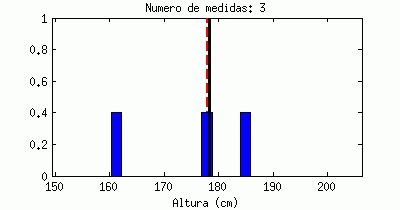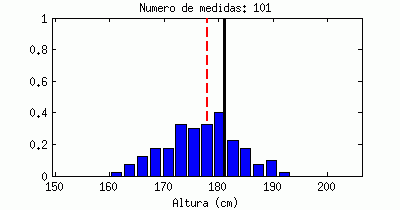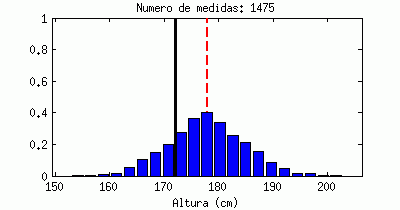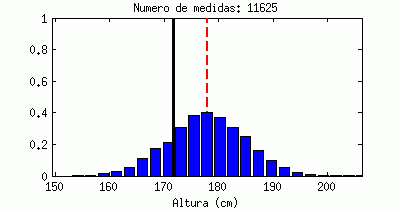
Está claro que un valor medio, por sí sólo, apenas nos dice nada. La animación siguiente muestra una línea negra que va saltando emulando «medidas de altura» que hiciéramos a hombres al azar, en comparación con el valor medio (la línea roja discontinua). Cada «salto» que da sería una medida a un nuevo individuo:
Estoy seguro que todos reconoceréis la forma a la que tiende este contador, llamado «histograma«: tiende a una campana de Gauss (distribución de probabilidad Gausiana, también llamada normal).
 |
| De estas dos medidas, la de la derecha tiene mucha menos incertidumbre ya que los valores se dispersan menos. |
3. Ejemplo: encuestas de intención de voto
Existen teorías estadísticas muy bien estudiadas (ver [1,3]) que nos ayudan a diseñar encuestas a partir del margen de error que deseamos obtener. Obviamente, cuanto más seguros queramos estar a más individuos habría que entrevistar, llegando al extremo de preguntar a toda la población si queremos reducir la incertidumbre a cero.
Pero eso se lo dejamos a las empresas de demoscopia. Nos ponemos en el papel de haber recibido el resultado de una encuesta. Por ejemplo, la que antes mencionaba de de El País.
Esta es la estimación del voto según las encuestas de los últimos meses (lo siento, por comodidad en el eje horizontal en vez de fechas he puesto números, mirad el gráfico original de El País para fechas):
En el artículo del periódico se hacen una serie de afirmaciones sobre estos datos, por ejemplo:
- Que el PP se desploma en el último mes, cayendo 8% su intención de voto. Esta afirmación se basa en que se pasa de un 46,3% en marzo a un 38,1% en abril.
- UPyD e IU son los que recogen el voto perdido por PP y PSOE. En el último mes IU sube del 9,1% al 11,6%, mientras que UPyD sube del 5,1% al 5,9%.
Viendo las gráficas, también podríamos decir, por ejemplo, que el PP no ha parado de subir desde enero de 2011 (43,1%) hasta enero de 2012 (46,4%).
Pues bien: aunque todas estas afirmaciones parezcan de lo más razonables, no hay que olvidar lo fundamental:
Los valores de estimaciones de voto son eso: estimaciones. Los datos reales podrían bien ser mayores que menores. En otras palabras: cada valor de intención de voto tiene su incertidumbre.
He creado una animación que ayudará a interiorizar de qué estamos hablando: teniendo en cuenta las fórmulas que luego veremos, la incertidumbre de las estimaciones de votos significan que los datos reales (desconocidos) bien podrían ser cualquiera de todos estos que aparecen como bailando alrededor de la estimación de la encuesta:
Lo que estamos viendo no es ni más ni menos que los efectos de que las estimaciones de voto no sean perfectas, sino que tengan una desviación estándar (un sigma) de incertidumbre.
En concreto, para una encuesta basada en N entrevistas, la desviación estándar de una opción cuya estimación es del P% se puede demostrar que es aproximadamente (ver [2,3] y la nota (*2) ):
Si queremos saber a qué «margen de error» se corresponde esto, tenemos que decidir hasta qué «seguridad» queremos llegar, y multiplicar esta sigma por el número correspondiente. Un ejemplo: en una entrevista de N=1000 llamadas telefónicas, una opción recibe un apoyo del p=60%, la desviación estándar de ese porcentaje de apoyo será:
Por lo que con un 95,5% de seguridad, a lo que corresponde un margen de error de ±2σ como vimos antes, el apoyo real de esa opción está entre 60% ± (2 x 1,55%) = 60% ± 3,1%, es decir entre el 56,9% y el 63,1%. Por cierto, en las fichas técnicas de las encuestas solamente se da el margen de error para el peor caso posible, que se puede demostrar es el de una opción apoyada por el 50% de los individuos (¡a eso se refiere el «famoso» p=q=50!), pero nada nos impide usar la fórmula que doy arriba y saber la incertidumbre exacta.
Siguiendo con la gráfica de antes, el efecto de la incertidumbre se ve aún más claro si vemos todas las posibilidades simultáneamente. Recuerda que lo que la encuesta nos está diciendo es que el valor real podría ser cualquiera de entre estas marañas:
4. Comparando valores
¡Ya llegamos a la parte interesante! Aunque sea un poco más abstracto, también existen los conceptos de desviación estándar y de margen de error para las diferencias entre dos valores a comparar, p.ej. la ventaja en votos entre dos partidos. Y no es tan sencillo como sumar las dos desviaciones estándar de cada valor a comparar; ojo, que es un error bastante común.
Está claro que es muy importante conocer el margen de error de una ventaja para determinar si ésta es estadísticamente significativa… o no, en cuyo caso podemos tratar al lector como si fuera inteligente y decirle que «existe una ventaja de tal y tal, pero no es estadísticamente significativa». Además, si fuera redactor, estaría orgulloso de poder dar información de calidad científica… (¡ahí lo dejo!).
Fijémonos en el caso concreto de la encuesta de El País, en el que IU aventaja claramente con un 11,6% a UPyD que sólo tiene un 5,9% para ese mismo mes, en la misma encuesta.
Ingenuamente, parece indudable que IU ganaría a UPyD ya que, vaya… ¡tiene el doble de votos!
Pero debemos asegurarnos y nunca dar nada por sentado, ya que ambos valores de intención de voto tienen su incertidumbre. Y además… están correlados, ya que no son independientes. Es decir, si IU en la realidad tuviera un 1% menos de votos, ese 1% bien podría ir a parar a UPyD. Lo que no es probable es que ambos tuvieran, simultáneamente, un 1% más de votos que lo estimado ya que lo que uno gane lo podría perder el otro. A eso es a lo que se llama correlación estadística.
Para casos como este en que comparamos porcentajes de apoyo a distintas opciones A y B, dentro de una misma encuesta, se demuestra que la desviación estándar de la ventaja entre A y B, dando los porcentajes p_A y P_B en tanto por ciento, es:
En el caso de la ventaja de IU al UPyD, al que le saca 11.6% – 5.9% = 5.7%, obtenemos con la fórmula de arriba una sigma del 1.31% para dicha ventaja.
Ahora, aplicamos el criterio de relevancia estadística, que consiste en ver en «cuántas sigmas» consiste la diferencia. Es decir, en dividir:
Decimos entonces que la ventaja de IU a UPyD es de «4.35 sigmas», ¡lo cuál es mucho! Para quienes sepan de estadística, este número ya les dice mucho, pero de cara a un público generalista estaría bien usar las siguientes conversiones entre «número de sigmas» y probabilidad de que «lo que estamos probando no sea cierto»:
|
Número
de sigmas |
Probabilidad
de error en la |
Probabilidad de que
la hipótesis planteada sea cierta
|
|
0,5 σ
|
61,71%
|
38,29%
|
|
1 σ
|
37,73%
|
68,27%
|
|
1,5 σ
|
13,36%
|
86.63%
|
|
2 σ
|
4,45%
|
95,45%
|
|
2,5 σ
|
1,25%
|
98,76%
|
|
3 σ
|
0,27%
|
99,73%
|
|
4 σ
|
0,0063%
|
99,9937%
|
|
5 σ
|
0,0001%
|
99,9999%
|
Es decir, que existe una probabilidad del ~99,9% de que IU ganase a día de hoy a UPyD, como nos decía el sentido común. Ojo, porque sólo sabemos con esa seguridad que ganaría, pero no por cuánto ganaría. Calcular eso ya nos obligaría a hacer cuentas más complejas, así que lo dejaremos por hoy (si alguien está interesado, ¡que consulte a su amigo matemático más cercano!).
Como normal general se usa como criterio que todo lo superior a 2 sigmas (o 3 sigmas siendo muy conservador) ya se puede dar como bastante seguro. Únicamente para hechos muy singulares se exigen 4 sigmas o más antes de aceptarlos como ciertos, como ocurre con la detección del famoso bosón de Higgs en el acelerador LHC.
Ahora bien, esto era para comparar dos partidos políticos en la misma encuesta. Si queremos comparar la evolución de una opción a lo largo del tiempo, debemos usar esta otra fórmula para la incertidumbre:
Donde p_A y p_B son el apoyo (en %) que recibió en los momentos A y B, y N_A y N_B son el número de entrevistas que se realizaron en cada una de dichas encuestas, dato que podría haber variado, especialmente en esta época de crisis en que cada año se recorta más en todo.
Veamos si realmente UPyD ha subido este último mes, al pasar de un 5,1% a un 5,9%. Tenemos un incremento del 0,8% pero la sigma es de σ=1.02%, por lo que el aumento es de 0,8 / 1,02 =0.78 sigmas, muy lejos del valor de 2 sigmas usado como umbral. De hecho, mirando la tabla de arriba vemos que la hipótesis de que UPyD haya subido en votos tiene menos de un 60% de probabilidad de ser cierta, luego su incremento no es estadísticamente significante.
5. Andaluzas de 2012
Los resultados de las elecciones andaluzas de 2012 (ver resultados) fueron toda una sorpresa, ya que parecían contradecir todo lo que las encuestas habían pronosticado hasta una semana antes.
Usando las fórmulas que hemos aprendido arriba, vamos a analizar qué cambios fueron realmente significativos entre las predicciones de las encuestas y el resultado real. Para ello, voy a usar los datos de la encuesta de La Razón basada en 2700 entrevistas. Estos son los votos esperados por cada opción política, y su desviación estándar:
Y estos fueron los resultados reales de las elecciones, junto a la distancia (en número de sigmas) a la predicción de la encuesta y la correspondiente probabilidad de que la estimación de voto fuera errónea:
PP=40.66% => 5.56σ => 99.99999730225 %
PSOE=39.52% => 3.56σ => 99.96291 %
IU=11.34% => 2.10σ => 96.42711 %
UPD=3.35% => 0.89σ => 62.65 %
Abs=37.77% => 5.60σ => 99.99999785 %
Lo esperable es que todas las probabilidades de predicciones erróneas hubieran sido bajas… pero obviamente no fue así. En cambio, únicamente la predicción de UPyD estuvo acertada, y siendo generosos, la de IU por los pelos. El resto de predicciones (PP, PSOE, abstención) fueron absoluta basura: casi al 100% fueron erróneas.
Distintas empresas de demoscopia hicieron análisis independientes y llegaron a predicciones compatibles entre sí. Luego, sólo veo tres explicaciones posibles a este desastre de las predicciones:
- O todas las empresas se equivocaron en algo importante a la hora de planificar el muestreo, lo que implicaría que todas ellas dispusieron de datos erróneos sobre la estructura de la población (clases sociales, edad, etc.),
- o realmente pasó algo que hizo cambiar su voto a mucha gente en la última semana,
- o una combinación de estas dos razones.
Asumiento que las encuestas fueron correctas, la explicación más probable de qué cambió en la última semana serían aquellos cambios de mayor sigma:
Con una certeza del ~99,99999%, un 5,34% de andaluces, simpatizantes del PP, no les votaron finalmente, mientras que un 5,37% de andaluces más de lo esperado se quedaron en casa y no fueron a votar; lo que se corresponde con hechos de 5,56σ y 5,60σ, respectivamente.
Obviamente, esto no quiere decir que todo el aumento de la abstención se nutriera de potenciales votantes del PP, ya que sólo hablamos en términos estadísticos y no hay forma de identificar a quienes dejaron de ir a votar… aunque podamos suponerlo.
Irónicamente, todo apunta a que la perspectiva de una victoria demasiado segura fuera el origen del descalabro del PP.
6. Calculadoras
Están en una entrada aparte por comodidad.
Referencias:
- «NTP 283: Encuestas: metodología para su utilización». Margarita Oncins de Frutos. Ministerio de Trabajo y Asuntos sociales de España. (PDF)
- Charles H. Franklin, «The ‘Margin of Error’ for Differences in Polls». 2002 (PDF)
- Scheaffer, R.L., Mendenhall III, W., Ott, R.L. & Gerow, K. «Elementary survey sampling». Duxbury Pr, 2011 (Google Books)
(*) Sólo sería exacto si la distribución de probabilidad fuera exactamente una Gausiana. A los que no les den miedo las mates, recomiendo que lean sobre la distribución chi cuadrado.
(*2) Realmente el «N» sería «N-1» pero como siempre serán valores grandes el error de usar N a cambio de no complicar la fórmula es asumible