Movimientos de robots y variedades matemáticas (manifolds)

Cuando se trata de robots no podemos olvidar que su objetivo fundamental siempre estará de alguna manera relacionado con moverse. Ya se trate de brazos robóticos como las que se encuentran en las fábricas de coches, encargadas de soldar o de alimentar con piezas a otras máquina, o se trate de robots móviles, que se mueven a ellos mismos por todo el espacio de trabajo.

«¿Por dónde tiro que no la líe?» (Créditos: 1)

En general, la posición y la orientación de un robot con N grados de libertad se puede parametrizar completamente por medio de N coordenadas. Sin embargo, hacer que el sistema se mueva desde una configuración inicial q0 a un estado objetivo q1 puede no ser tan sencillo como parece. Para empezar, pueden existir obstáculos en el camino, así que se deben considerar para evitar colisiones. En segundo lugar, tenemos lo que se llaman restricciones no holónomas. Los vehículos con ruedas son un ejemplo perfecto. Es fácil entender que la posición y orientación de un vehículo terrestre se pueden definir perfectamente mediante tres coordenadas (la posición en 2D sobre el suelo, más un ángulo para la orientación). Pero el vehículo en sí, considerado como un mecanismo, sólo tiene dos grados de libertad: la posición de cada una de las dos ruedas motrices si es diferencial, o la velocidad y la dirección del volante en automóviles comerciales. Existe una relación compleja (una ecuación diferencial) entre las velocidades de las ruedas y la posición en la que el vehículo termina. ¡Basta con pensar en lo difícil que se hace aparcar en un espacio estrecho!

Es evidente que necesitamos algo diferente cuando existen estas limitaciones. La propuesta de Jaillet y Porta, publicada recientemente en la revista IEEE Transactions on Robotics [2], en gran medida se basa en la comprensión de la geometría abstracta de las variedades. Resulta que el espacio de estados de todas las configuraciones permitidas es una variedad, de ahí la importancia del concepto.


Pero, ¿qué son exactamente las variedades? Informalmente, se puede pensar en ellas como en espacios (2D, 3D, etc) que parecen euclídeos a nivel local y que «viven» incrustados en un espacio de mayor dimensionalidad. Un ejemplo perfecto es la superficie de la Tierra: es una variedad 2D porque, bueno … ¡es una superficie! Sin embargo, «vive» en un mundo 3D (el planeta visto en su conjunto), por lo que tiene una curvatura que, aún siendo muy pequeña, se puede ver cuando observamos grandes porciones de la superficie. Una área pequeña de la superficie podría aproximarse muy bien como una superficie perfectamente plana.

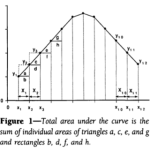
Con esta idea en mente, podemos tomar una variedad entera y construir lo que se llama un atlas de aproximaciones lineales locales (los llamados mapas o charts de los espacios tangentes) para un conjunto discreto de ubicaciones sobre la variedad:

(Arriba) La variedad es la línea negra sólida, sobre la que se construye un mapa alrededor de x_i. Para un punto lejano en la variedad, como xj, la aproximación introducida por el mapa lineal puede dar lugar a grandes errores. (Abajo) Cuando eso ocurre, se debe crear un nuevo mapa. (Fuente: [2])