Si se busca en Internet «alineamiento» y «2012» aparecerán todo tipo de desinformaciones mezcladas con datos reales, así que voy a intentar hacer un repaso de los errores más comunes para desmontarlos con cálculos, simulaciones y vídeos del estado de los astros en las fechas supuestamente señaladas. En concreto, siempre aparece el solsticio de invierno (21 diciembre) como día clave.
Sólo voy a hablar de los astros en sí, no de la supuesta profecía Maya, que en realidad solo habla de terremotos y el fin de un calendario para el comienzo de otro ciclo (y nadie puede asegurar ni el día exacto de tal evento, ni que ellos pudieran calcularlo tan exactamente). Sobre los Mayas y su calendario en sí recomiendo este concienzudo análisis.
ALINEAMIENTO PLANETARIO
Primeramente, se pueden leer cosas del estilo: «va a ocurrir un alineamiento planetario«. Usando Celestia (en repositorio para Ubuntu) he simulado las posiciones de los astros el 21 de diciembre de 2012 y es evidente que no ocurre ninguna alineación en particular:
A mi parecer, el tema de los planetas es un puro disparate de quienes oyeron algo sobre el alineamiento con el plano galáctico (que sí es real y ahora hablo de él) y lo confundieron con los planetas. Aún así, me he tomado la molestia de calcular la fuerza adicional que podría hacer el más fuerte alineamiento posible (con Jupiter en su máxima aproximación a la Tierra), y resulta ser de 10.000 veces más débil que el tirón que el Sol nos hace todos los días, por lo que su efecto podría ser, como mucho, una minúscula (seguramente ni mensurable) variación de las mareas. Y repito, ésto no ocurre el 21 de diciembre de 2012, aunque según mis cálculos (espero que correctos) sí ocurre cada 10.1 años, así que no debe ser muy grave si estamos aquí vivos.
ALINEAMIENTO CON EL PLANO GALÁCTICO
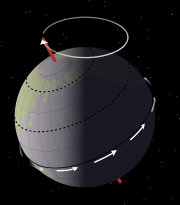 Debido al movimiento de precesión de nuestro planeta, su eje de rotación va, a su vez, rotando describiendo un cono al igual que hace una peonza. Debido a este movimiento, el equinoccio de invierno (una posición que alcanza el Sol durante ese día en el cielo) va variando en un ciclo que se repite cada ~26.000 años. Los hay que defienden que los Mayas usaban este ciclo como una medida fundamental en sus calendarios (lo que no todos los expertos creen), y más aún, que en 2012 se produce el cambio de un ciclo al siguiente.
Debido al movimiento de precesión de nuestro planeta, su eje de rotación va, a su vez, rotando describiendo un cono al igual que hace una peonza. Debido a este movimiento, el equinoccio de invierno (una posición que alcanza el Sol durante ese día en el cielo) va variando en un ciclo que se repite cada ~26.000 años. Los hay que defienden que los Mayas usaban este ciclo como una medida fundamental en sus calendarios (lo que no todos los expertos creen), y más aún, que en 2012 se produce el cambio de un ciclo al siguiente.
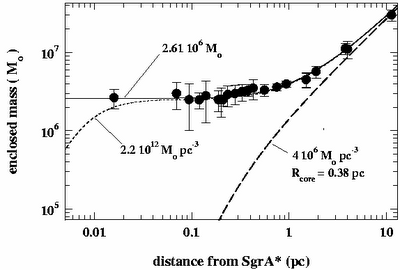
EFECTOS GRAVITATORIOS DE LA «ALINEACIÓN»
Si se aplica al caso de un campo gravitatorio da lugar a la ley de Gauss de la Gravedad:
donde G es la constante de gravitación. Esta fórmula representa una simplificación bestial al problema de estimar la fuerza con que la Galaxia tira de nosotros, ya que nos dice que solamente hay que tener en cuenta cuánta masa hay dentro de un volumen, p.ej. una esfera, dando exactamente igual como esté distribuida ésta:
Si ahora sumamos el campo gravitatorio g sobre una superficie de una esfera de radio R, tenemos:
donde el signo menos viene de que los vectores g y dA son paralelos pero de direcciones opuestas. Igualando las dos últimas ecuaciones podemos despejar el valor de |g|, o sea, de la aceleración que sufriría una masa de prueba en el punto en cuestión:
Y sustituyendo los datos numéricos:
Este valor se debe comparar con la aceleración producida por la gravedad de la Tierra, que es bien sabido que vale:
que es una medida de la «fuerza» con que la Tierra tira de cualquier cosa hacia abajo. Pero en cualquier momento del día o la noche, además estamos sintiendo el tirón del Sol (hacia arriba o abajo, respectivamente). El Sol tira con una aceleración de:
Fuentes:
- http://www.mpe.mpg.de/ir/GC/prop.html
- http://www.astro.uu.nl/~strous/AA/en/2012.html
- http://www.instituteofmayastudies.org/Milbrath2012.pdf